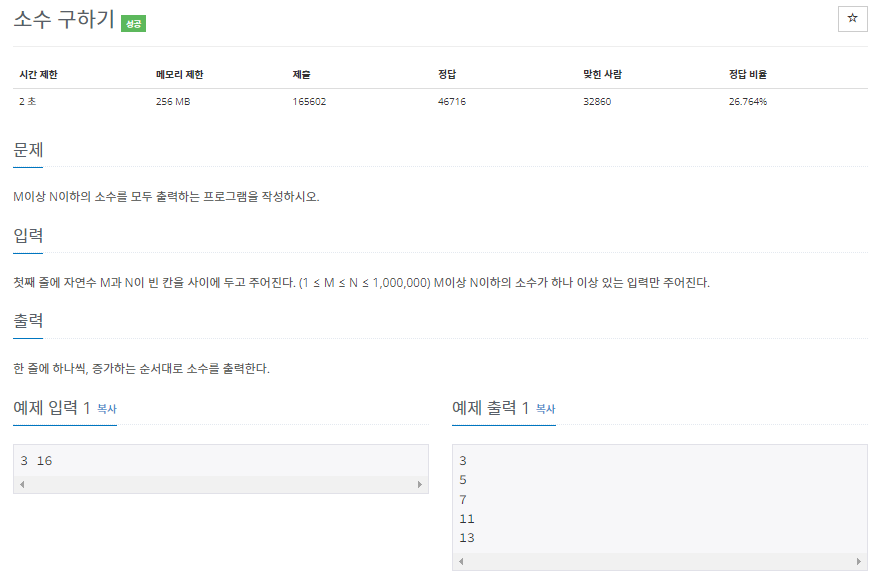
소수임을 판별해야 하는 숫자가 많을 때는, 이를 일일이 확인하기 보다는 에라토스테네스의 체를 사용하는 것이 좋다.
class Program
{
static void Main()
{
//입력
string[] input = Console.ReadLine().Split();
int m = int.Parse(input[0]);
int n = int.Parse(input[1]);
//에라토스테네스의 체
bool[] isNotPrime = EratosSieve(n);
//출력
StreamWriter sw = new(new BufferedStream(Console.OpenStandardOutput()));
for (int i = m; i <= n; i++)
{
if (!isNotPrime[i])
sw.WriteLine(i);
}
sw.Close();
}
static bool[] EratosSieve(int n)
{
bool[] isNotPrime = new bool[n + 1];
double sqrtN = Math.Sqrt(n);
//0과 1은 소수가 아니다
isNotPrime[0] = isNotPrime[1] = true;
for (int i = 2; i <= sqrtN; i++)
{
//이미 지워진 수로는 반복할 필요가 없다
//예를 들어, 4의 배수는 이미 2의 배수를 지울 때 모두 지워졌으므로 굳이 반복할 필요가 없다
if (isNotPrime[i])
continue;
//자기 자신은 지우지 않으므로 초기값은 i + i가 된다
for (int j = i + i; j <= n; j += i)
{
isNotPrime[j] = true;
}
}
return isNotPrime;
}
}
소수를 판별할 때와 마찬가지로, 에라토스테네스의 체 또한 상한치의 제곱근 까지만 루프를 돌리면 된다.
예를 들어 상한치가 100이라면 10까지만 반복하면 된다는 뜻이다.
11부터는 반복할 필요가 없다. 이전의 반복에서, 2 x 11 / 3 x 11 / 4 x 11 / 5 x 11 ... 을 통해 100보다 작거나 같은 11의 배수들을 모두 지웠기 때문이다.
그렇게 2부터 시작하여 2의 배수들을 모두 지우고, 그 다음 지워지지 않은 3의 배수들을 모두 지우고, 4는 2의 배수라 지워졌으니 무시하고, 또 5의 배수들을 모두 지우고... 를 반복한다. 이때 자기 자신은 지우지 않는다.
그러면 지워지지 않은 수는 모두 소수가 된다.
아래 그림은 에라토스테네스의 체가 작동하는 모습이다.

'문제 풀이 > 백준' 카테고리의 다른 글
| 백준 10872 C#) 팩토리얼 (0) | 2022.05.12 |
|---|---|
| 백준 9020 C#) 골드바흐의 추측 (0) | 2022.05.07 |
| 백준 11653 C#) 소인수분해 (0) | 2022.05.06 |
| 백준 2839 C#) 설탕 배달 (0) | 2022.05.06 |
| 백준 10250 C#) ACM 호텔 (0) | 2022.05.05 |




댓글