대부분의 언어에는 이미 거듭제곱 함수가 내장되어 있지만, 가끔씩 내가 직접 만들어야 하는 상황이 생긴다. 예를 들어 Mod 연산이 필요한 문제라든가...
그래도 구현이 어렵진 않기 때문에 한번 외워두면 두고두고 써먹을 수 있다.
거듭제곱의 계산은 (1)반복문 과 (2)재귀 로 구현할 수 있다. 각자 편한 방식을 택하자.
(1) 반복문
여기서는 간단하게 느낌만 설명하겠다.

3^13을 예로 들어보자.
지수 13을 이진수로 바꿔서 생각하면, 우리는 3^13을 아래와 같이 표현할 수 있다.

지수법칙에 의해 3개의 항으로 나누어졌다.
반복문에서 행해지는 작업은 위 항들을 구하는 것이다.
public static int pow(int a, int b)
{
int result = 1;
while (b > 0)
{
if ((b & 1) == 1)
result *= a;
a *= a;
b >>= 1;
}
return result;
}
구체적인 원리가 궁금하다면 구글에 Square and multiply 혹은 Exponentiation by squaring 을 검색해보자. 여기서는 너무 길어질 것 같아서 설명하지 않겠다. (참고로 전자는 주로 암호학에서 사용하는 용어인 듯하다.)
(2) 재귀
구체적으로는 분할정복 기법을 사용하며, 아래의 조건에 따라 진행된다.

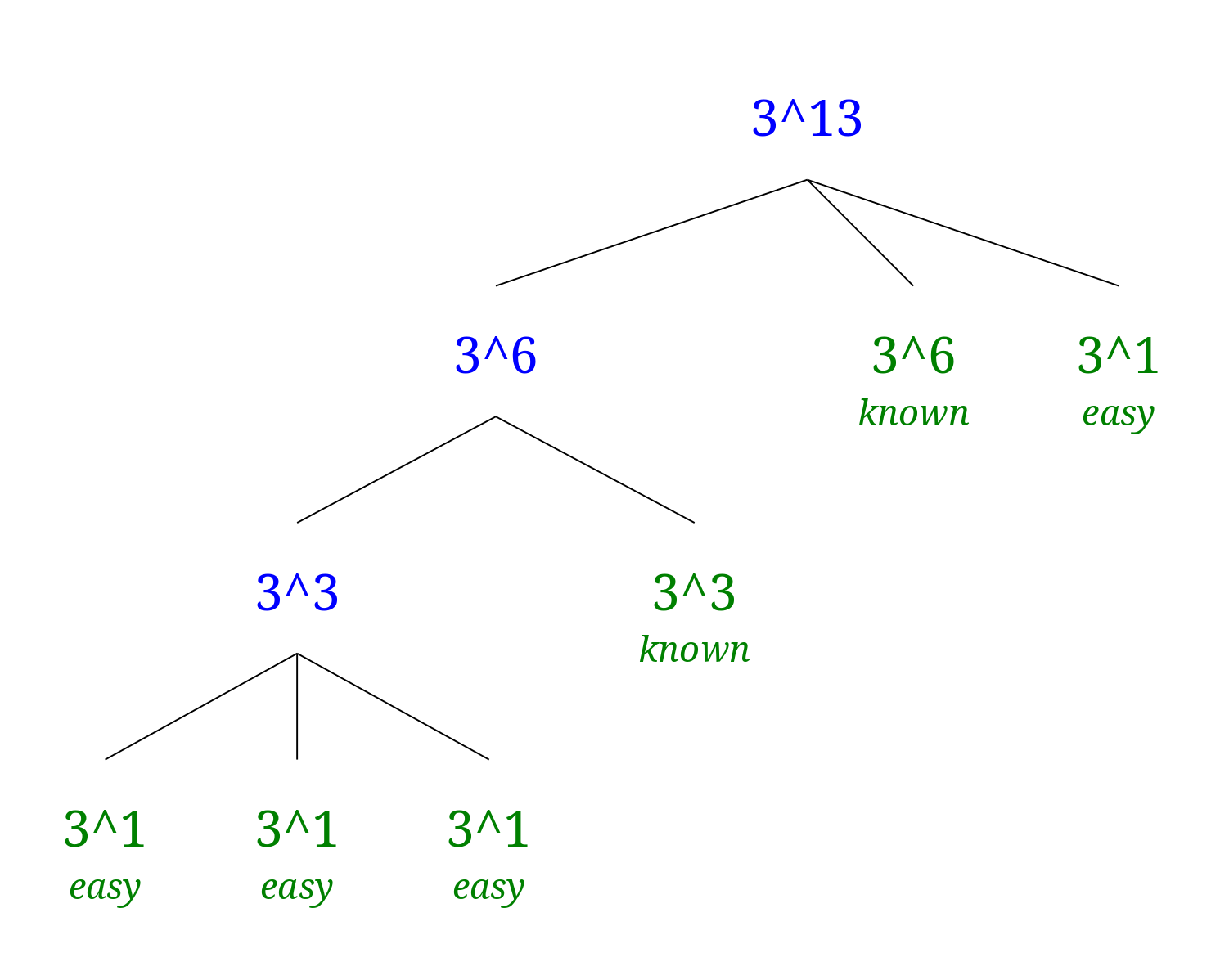
예를 들어, 3^13은 조건에 따라 아래와 같이 표현할 수 있다.

그러면 3^6을 한번 계산하는 것으로 3^13에 대한 계산을 끝마칠 수 있다.
이해가 잘 안된다면 아래의 트리를 참고하자.
public static int pow(int a, int b)
{
if (b == 1)
return a;
int temp = pow(a, b / 2);
if ((b & 1) == 1)
return temp * temp * a;
else
return temp * temp;
}
참고로 이 코드에서는 b가 0일 때를 고려하지 않았다. 만약 수정하고 싶다면 b가 1일 때를 b가 0일 때로 바꾸고, a가 아닌 1을 반환하도록 하면 된다.
'CS > 알고리즘' 카테고리의 다른 글
| 정렬 #3) 삽입 정렬 (1) | 2022.10.04 |
|---|---|
| 정렬 #2) 선택 정렬 (1) | 2022.10.04 |
| 정렬 #1) 버블 정렬 (1) | 2022.10.04 |
| 정수의 각 자릿수를 다루는 방법 (C#) (0) | 2022.08.28 |
| 매개 변수 탐색(parametric search, 파라메트릭 서치) (3) | 2022.08.09 |




댓글